転がり玉軸受は基本的に回転することによって機能をはたしますが、回転することによって振動も発生します。
回転数に依存して周波数が変化する振動を、「強制回転による振動」といいます。
転がり玉軸受の強制回転による振動計算
振動は、アキシアル方向、ラジアル方向、回転方向の3方向に発生します。転がり玉軸受が使用される商品によってはこれらの振動が性能に大きく影響します。
また、これらの振動は振動エネルギーとして軸まわりの構成部品の固有振動を励振させることもあります。
商品特性を理解して、軸受の選定・仕様の決定をする必要があります。
内輪回転の場合の計算式
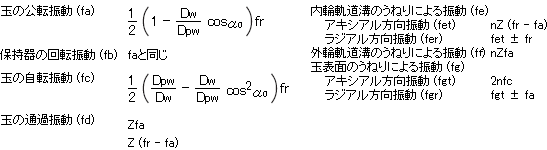
外輪回転の場合の計算式
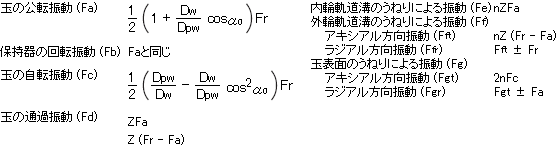
Dw : 玉径 (mm)
Dpw: ピッチ円径 (mm)
α0 : 呼び接触角 (°)
α0 : 呼び接触角 (°)
Z : 玉数
n : 整数
fr : 内輪回転速度 (Hz)
Fr : 外輪回転速度 (Hz)
n : 整数
fr : 内輪回転速度 (Hz)
Fr : 外輪回転速度 (Hz)
なお簡易計算として、cosα0 = 1 としても問題ありません。
これらの計算式による解析の例を、次に示します。
例1: R-1560X2ZZの場合、玉の公転振動は内輪を1800min-1で回転させたとき上記計算式より、
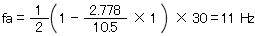
となります。
例2: R-1560X2ZZの場合、外輪の軌道溝の変形、内輪の軌道溝の形状が6、7、8角形となった時、上記計算より求めた振動位置での振幅が大きくなることが分かります。 (図15-3、15-4、15-5、15-6)。
正常な回転方向振動
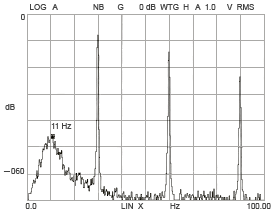
図 15-1
玉の相互差が大きい場合の回転方向振動
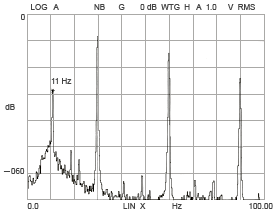
図 15-2
外輪軌道溝変形 (3角形)
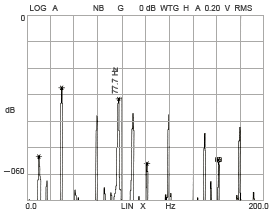
図 15-3
内輪軌道溝6角形
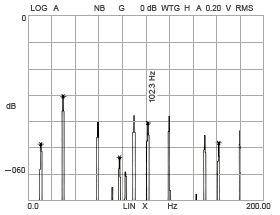
図 15-4
内輪軌道溝7角形
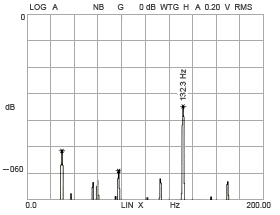
図 15-5
内輪軌道溝8角形
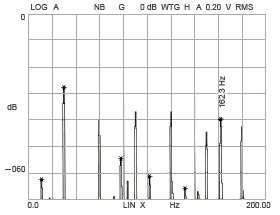
図 15-6
関連ページ
ミネベアミツミの技術情報やイベント情報をはじめ、お役立ち情報をお届けします
